Místo matematiky a logiky řeším věci počítačovou silou

MyEgo.cz

Místo matematiky a logiky řeším věci počítačovou silou

Technologie 25.11.07

Nevím zda je to programátorská deformace za 20 let co se tomu věnuji, nebo prostě člověk zapomíná věci z desítky let vzdálené školy, ale uvědomil jsem si, že hodně dříve běžných úkonů řeším nyní prostě jinak.

Než abych se zamýšlel nad logickým či ryze matematickým řešením, napíšu si raději rychle počítačový algoritmus (aka program), který to během pár minut či sekund vypočítá místo mě.

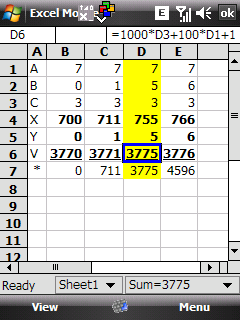
Vezměte si třeba tuto triviální úlohu ze 4. třídy ZŠ (tedy pro devítileté děti), cílem je za stejná písmena dosadit stejné číslice, za různá písmena různé číslice tak, aby výsledek vycházel a výpočet byl tedy pravdivý: ABB * B = CAAB.

Koukal jsem na to 30 sekund, řešení jsem neviděl, tak jsem vytáhnul HTC Kaiser telefon, spustil mobilní Excel a místo počítání z paměti to nechal na Excelu. Hotovo (i s psaním vzorečků) za dvě minuty. Já vím, určitě to jde udělat inteligentněji než "hrubou silou", ale já jsem s tímto řešením spokojen. Dosáhl jsem výsledku, a o to jde.

Pokud někdy nestačí Excel na desktopu a jeho parádní "Solver" (úžasná věc, doporučuji vyzkoušet), vytahuji vyšší kalibr, tedy Matlab, s tím se už dá vyřešit naprosto vše (opět metodou "hrubá síla").

Vlastně "hrubou sílu" (programování) místo matematického řešení mám rád už dlouho.

Před patnácti lety, když jsem dělal přijímačky na čtyři různé VŠ zároveň (práva, ekonomie a matematická informatika v Brně, plus ekonomie ve Zlíně; aneb opravdu jsem netušil v 18 letech co chci dále dělat, tak jsem to zkoušel; na všechny jsem se samozřejmě dostal v první desítce), tak jsem právě ve Zlíně dostal k řešení dost složitou rovnici, v níž figurovalo x^5, faktorial x a pár dalších prvků. Vůbec jsem netušil co s tím dělat a jak to zjednodušit (prý to vypočítali nakonec jen 2 uchazeči z několika set), tak jsem vzal programovatelnou kalkulačku TI-81 (naštěstí povolenou u přijímaček), zkusmo odhadl výsledek, napsal si pár řádků kódu na metodu půlení intervalu a během pár minut měl 3 čísla, která do oné rovnice pasovala. Heuréka!

Netušil jsem, jak se k tomu postaví hodnotící profesor, čekal jsem spíše "průser", ale dopadlo to dobře. Programátorský algoritmus místo matematického jej zjevně zaujal, nakonec jsem byl jeden ze dvou lidí který nabídl správný výsledek, byť jsem k němu došel "oklikou".

Podobně je to s dalšími počítačovými věcmi, které zjednodušují dnes a denně život. Nevím jak se jede ke klientovi, i když jsem tam už 5x byl, vždy si totiž pustím TomTom 6 Navigator na telefonu, ten mi během pár sekund vypočítá optimální trasu, a já poté jen poslouchám povely typu "zabočte doprava" a "jeďte tři kilometry rovně".

Někde v pozadí tuším, že řešit věci "hrubou programátorskou silou" není asi to pravé, není to "čisté", nicméně vede to k výsledku stejně dobře jako to "čistá" cesta, a mnohdy dokonce podstatně rychleji.

Můj mozek není schopen některé úlohy řešit dostatečně rychle, ale je schopen je bleskurychle algoritmicky popsat a předhodit počítači k řešení.

A jak jste na tom vy? Přemýšlíte nebo programujete?

Komentáře

1 Peter 25.11.07, 04:11:42

Hm... veľmi zaujímavá úvaha... ja som mal na prijímacích skúškach tiež veľmi... "hrubú" kalkulačku, kým ostatní ťukali ako besní, ja som si rozpísal premenné, zadal do zložených tvarov ich hodnoty a spočítal... trvalo mi to asi tak minútu.
Sme v predsa v treťom tisícročí, tak podľa toho aj žime! :) Ja na tom nevidím nič zlé.
2 Miroslav Navrátil 25.11.07, 05:11:03

Svatá pravda!!! :-) Shodou náhod mi teď leží na disku PHP kód pro "vypočítání" dvou příkladů z matematické olympiády. :-)) Ovšem zajímalo by mě, jestli mi to p. profesorka z matematiky uzná.
3 Morpheus 25.11.07, 05:11:12

IMHO každá generace využívá prostředky, které má k dispozici... Jasně, že "staré gardě" to může připadat, že nová generace je hloupější, když řeší věci takto, nicméně, proč ne?
Můj obor je strojařina, na fakultě je celkem jasně poznat, kdo je "stará garda" a kdo je schopný používat nové metody... Osobně nechápu požadavky zejména starších zapšklých dědků, co chtějí všechny rysy v ruce s argumentem "počítač nemáte po ruce vždy"... Měl bych asi umět danou věc v ruce NAČRTNOUT, ovšem nevidím smysl v tom, nutit někoho ručně rýsovat. Proč taky? Já osobně mám asi tak 100x častěji k dispozici počítač s AutoCADem, než rýsovací prkno :-)
Samozřejmě, že jisté "základní znalosti a dovednosti" by asi člověk mít měl (nerad bych, aby děti za chvíli vytahovaly i na výpočet typu 4x5 kalkulačku), ale jinak nevidím důvod v tom, že někdo použije poněkud jiné prostředky k tomu, aby dospěl k výsledku...
Nota bene třeba ten příklad s faktoriály a x^5 etc. - je hezké, když to člověk bude počítat "z hlavy", jenže v praxi to stejně bude řešit s využitím výpočetní techniky, kde se rovnice řeší jak? No přeci numericky, rozhodně ne stylem "mrkni na to, zauvažuj, jak by se to dalo pokrátit", to se programuje docela blbě :-)
4 Libor Foltýnek 25.11.07, 05:11:30

Řešil a řeším to podobně. Zrovna včera večer, vezl jsem z fotosrazu "kolegu" domů do části Brna, kam běžně nejezdím, tak než bych bloudil sídlištěm, nahodil jsem navigaci a bylo to v klidu.
Na druhou stranu, občas ji nechám doma, mohou dojít baterky, může se stát cokoliv, takže osobně se snažím trénovat i mozek (ne v orientaci, tu vím, že mám šílenou).
Je asi dobré, když člověk umí navrhnout řešení, ale že se mu nechce počítat integrály nebo násobit ručně velká čísla, je pochopitelné. Ale když lidi neví, jak se počítá objem koule a neznají převody jednotek, nepomůže jim sebelepší počítač, protože prostě nebudou umět ten algoritmus sestavit.
P.S. taková hezká hádanka: představte si ocelovou kuličku o průměru 1mm. A nyní si představte 1000 (tisíc) takových kuliček. Odhadněte, kolik váží.
Lidi běžně tipují stovky kg a přitom jsou to jen asi 4 gramy! (1000 kuliček je 10^3, 10mm = 1cm, tzn. 1000 kuliček o průměru 1mm vyplní krychli o hraně 1cm, tzn. objem 1ml, při hustotě oceli asi 7600kg/m3 je to asi 7.6 gramů, a protože jsou to koule a nevyplňují ten objem dokonale, je to míň)
Omlouvám se za příliš podrobný popis, ale rád bych, aby to pochopili úplně všichni :-))
5 Martin Falhar 25.11.07, 05:11:39

Zvláštní, nedávno jsem na podobné téma taky přemýšlel. Nejsem profi-prográmator, programování mám jenom jako koníček. Dospěl jsem však do stádia, že luštím hlavolamy ne pro jejich podstatu, ale jako zdroj problémů, který mohu algorytmizovat. Takže jsem si koupil malou stopu Eternity a celý poblázněný jsem si dělal SW, který mi to řešil. Kamenoužrout z IS MUNI to stejné a hromada podobných logických libůstek. I já mám stejný pocit jisté etické neshody, když dosáhnu řešení. Na druhou stranu mám klid na duši a pocit jakési "blahoslavené vyčůranosti" jak jsem to pěkně obešel a vyřešil. Příjde mi, že řešení určitého problému vyžaduje určitý stupeň koncentrace a kreativního osvícení hledané podstaty. Když to ale dělám SW cestou, tak ona koncentrace (někdy mnohdy i pobláznění) dozajista je, ale mám vnitřní pocit, že je to snadnější cesta, než kdybych to řešil papírem a tužkou. Skutečnost je taková, že mnohdy SW řešení je časově podstatně delší, ale na druhou stranu někdy objevím samotné "jádro pudla" v jeho nejryzejší logické podobě. Bohužel ta první možnost mi přijde častější. Jedná se o předání potravy PC ať si to nakouše jak chce a my mu jen řekneme jak - typický BFA (Brute Force Access/Attack). Pocit určité "nečistoty" řešení plyne v případech, kdy problém vyřešíme a nevíme přesně to zákulisí - nevyvinuli jsme dostatečnou mentální tenzi na dosažení a pochopení cíle. A o to jde. Právě to pochopení podstaty nám zjednoduší vnímání, svět je zase o něco méně složitý, a kdy nám pochopení přinese radost jak jsem sakra dobří. Genialita je v jednoduchosti, ne v PC síle. Jsme moderní lidé a máme dvojí myšlení: jak to vymyslím já nebo jak to vyřeší PC. Je to počátek degradace? PS: Jednoduše dojít k výsledku, jo? Hmm, že bych si na to udělal prográmek? ;-)
6 Martin Duratny 25.11.07, 05:11:41

[3] presne tak...živo si spomínam na časy, keď nás nútil profesor natvrdo pauzáky a perá a ideš...ešte šťastie, že nás s tým trápili len v prvom ročníku, potom už nás nechali pri počítačoch...
7 Martin Falhar 25.11.07, 05:11:51

[3] Pokud je nutné najít řešení, je libovolné, jaké použiješ prostředky. Výkres v CADu je jasná volba. Pokud ale jde o to počítání: když se nenaučíš myslet nad podstatou, jak chceš pak řešit složitější věci. PC ti udělá řešení, ale samotné řešení vyžaduje postupy, které se ti mohou v budoucnu hodit. Jak chceš ale zúročit zkušenost z jiných problémů, když jsi si žádnou neudělal?
8 Morpheus 25.11.07, 06:11:22

[8] Proto taky nepíšu, že by člověk měl všechno mastit v PC (ale ani není nutné mastit vše na papíře). Pokud je "alternativní" řešení efektivnější, proč jej nevyužít? Pokud mi půjde o to, něčemu se doopravdy naučit, tak se sám budu pídit po postupu, pokud je nalezení řešení problému jen prostředkem k něčemu jinému (například složení přijímaček - jen prostředek k tomu, aby člověku doopravdy umožnili studovat), nevidím problém v tom použít pomůcky...
9 Diagon Swarm 25.11.07, 06:11:42

Já jsem postoupil ještě dál. Já si složitější problémy zadefinuju v Prologu. Tím se dají řešit prakticky libovolné úlohy a problémy :-).
10 Martin Falhar 25.11.07, 06:11:48

[10] S těma přijímačkama je to jak s hlavolamem. Vyřešit za každou cenu! Ryzí machiavelismus - účel světí prostředky. Asi je možná škoda, že se nepříhlíží ke kreativitě řešení. Mnohdy by se tak dalo prázdno v hlavě nahradit prokázaním snahou řešit. No a dovednost použít PC k takovému účelu je jak dovednost s jakýmkoliv jiným nástrojem. Když se s tím naučíš, tak to používáš. A problém je někdy říct, že to co uděláš je práve efektivnější. Ale to bych se utrápil, kdybych měl řešit jenom "efektivně". Holt, když se kácí, lítají třísky. Takže když jde něco ztuha použije s k tomu co je dostupné a jak to komu jde. Pravdou ale je, že úspěšná řešení jsou ta levná a nenáročná - tedy ty, co řeši podstatu přímo.
11 Branislav Viest 25.11.07, 09:11:12

v mojom pripade je velmi zaujimave ze vsetko, bezne veci, davam do suvisu s PC a s programovanim. vsade vidim premenne, polia a podobne prkotiny. :D
12 Ruy Lopez 25.11.07, 10:11:31

Hmmm, u mne to funguje přesně naopak - většinu problémů řeším postupem Kouknu a vidím (obvykle rychlejší než Brutal force). Problém nastává v okamžiku, kdy nastane Kouknu a nevidím :-(
13 Radek Hulán 25.11.07, 10:11:41

[2] no, ono poté co člověk zná správný výsledek, už se (občas) snadněji dopracuje k postupu, jak jej získat jinak než numericky (programem).. Nějaký příklad z matematické olympiády jsem tak kdysi také řešil, prvně výsledek, a pak z toho odvodit postup ;-)
14 Vratislav Harabiš 25.11.07, 11:11:42

Radku vy jste si jen tak, jako výkonnou "kalkulačku", pořídil Matlab? Matlab také využívám hodně (mám školní licenci), a tak vím, že je doslova pekelně drahý. Taky jsem se už několikrát přistihl, jak dělám prográmky pro úplně jednoduché věci :-)
15 Radek Hulán 26.11.07, 12:11:10

[15] mám stále stařičký Matlab 6 ;) Dělal jsem na Masaryčce ještě ve verzi 4 nebo 5 analýzy cenných papírů (pohyb ceny, faktory cenu ovlivňující), a později si verzi 6 zakoupil na firmě. Stačí mí ale, nepotřebuji toho tolik, abych dělal velice nákladný upgrade na 2007b.
16 Adam Černý 26.11.07, 04:11:17

Možno programovat, ale až po hodinách/dnech/týdnech přemýšlení, kdy naleznu nejméně časově náročný algortimus. Problém je dle mého názoru takový, že matematici dokáží používat výpočetní techniku dobře, ale ryzí programátoři, kteří berou matematiku jako spíše vedlejší předmět, prostě nemají úctu ke krásným řešením.
Kdo jen řešil např. olympiádu z matematiky, anebo se zabýval nějakým problémem, chápe, že hledání nových cest, ale i pouhá aplikace matematických vět, je něco úžasného. A hlavně je na řešení problémů úžasné to, že pokud jej vyřešíte, zvláštním způsobem v sobě víte, že je to prostě správně, a to se při programování nedostaví, alespoň u mne nikoliv. Pěkně to vyjádřil Coffee.
Co se týče Morfea, nejde zde přeci o využívání CADů (ať již v 2D, anebo v 3D), ale o schopnost analyzovat problémy a řešit je. Ono vaše 4*5 je neskutečně závislé na individuu. Nemyslím si, že by prodavačka v konzumu měla zvládat parciální derivace, ovšem zvláště programátoři by měli studovat matematiku hlouběji, a tak třeba přicházet na mnohem efektivnější algoritmy.
17 Radek Hulán 26.11.07, 07:11:51

[17] myslím, že třeba na takové matematické informatice na MU v Brně se matematika studuje tak dostatečně, že se k programování člověk vůbec nedostane ;)
18 Miroslav Navrátil 26.11.07, 08:11:10

[14] Tak takhle jsem to taky občas dělal, je to docela paradox vědět výsledek a "nevědět" postup, nebo k výsledku dojít nějakou cestou, která se "nebere" (a teď se nebavím o opisování).

Twitter	Facebook
Instagram	LinkedIn

Místo matematiky a logiky řeším věci počítačovou silou

MyEgo.cz

Místo matematiky a logiky řeším věci počítačovou silou

Komentáře

Radek Hulán

navigace

kategorie

aktivní diskuse

nejčtenější články