Teorie chaosu v ekonomii?

Stephen Smale, jeden z nejprominentnějších matematiků 2. poloviny 20. století, se nechal slyšet, že jedním z nejdůležitějších úkolů matematiky v rodícím se století je uvedení teorie chaosu do ekonomie. Protože oba výše zmíněné obory jsou mou srdeční záležitostí, vyjádřím se podrobnějí k ambivalenci, jíž ve mne tento názor vzbuzuje.

Nebudu se tajit tím, že již pár let mám raději ekonomii než matematiku a statistiku, ač tomu zatím ještě delší dobu bylo naopak. Matematika je sice moc hezká, ale příliš vzdálená každodennímu životu kohokoliv krom relativně úzké skupiny lidí. První část předchozí věty pro ekonomii platí dvakrát a druhá část vůbec.

(S tou vzdáleností matematiky od běžného života to není jednoznačné. Drtivá většina „samozřejmostí“, jež dnes lidé každodenně používají k usnadnění svého života, by bez vysoké matematiky nikdy světlo světa nespatřila. K jejich používání znalost matematiky není nutná, stejně jako k ekonomickému jednání není nutná znalost ekonomie. Přesto však i běžní lidé přemýšlejí o problémech ekonomického charakteru, které se jich týkají, a to v rámci svého chápání ekonomických fenoménů. O matematice žádní normální lidé nepřemýšlejí :-)).  

Ekonomické jednání je každodenním chlebem všech lidských bytostí. Nejen té drtivé většiny, která každé ráno vstává do práce, aby prodala svou práci a nakoupila prostředek směny (peníze) za účelem jejich budoucího prodeje za jiné směnitelné statky. Týká se i toho posledního poustevníka žijícího mimo civilizaci, který se rozhoduje, čemu věnuje následujících deset minut svého času. Osobní čas je statek s omezenou zásobou, který je předmětem ekonomického jednání. Zvolit určitou činnost znamená vzdát se jakékoliv jiné.

Ekonomie není primárně „vědou o penězích“, o podnikání, o cenách na trhu - a už vůbec ne návodem ke zbohatnutí. Zabývá se ekonomickým jednáním, tj. jednáním ve světě, kde „pečení holubi nelétají do huby“. Jednáním ve světě, který není rájem a kde je nutno provádět volby, jaké omezené prostředky a v jaké kombinaci použít k dosažení určitého cíle. Peníze, cenový systém, podnikatelská role atd., jsou jen důsledky, nikoliv příčiny ekonomického jednání. To je zas důsledkem výše uvedené nerajské podstaty světa, který obýváme.

Znalost ekonomie, tj. pochopení ekonomického jednání, jeho důsledků a relevantních kauzálních řetězců v ekonomické interakci, může přispět k lepšímu rozhodování. Obecně však brilantní podnikatel nemusí korektně a už vůbec ne zcela chápat fungování ekonomického systému (tak tomu též zpravidla je). Stejně tak znalost ekonomie z nikoho neudělá dobrého podnikatele. Podnikatelská role vyžaduje zejména jisté osobní kvality, nikoliv detailní pochopení ekonomických fenoménů v jejich komplexnosti. (Na druhou stranu se nebojím tvrdit, že zdravý ekonomický rozum některých podnikatelů zřejmě produkuje kvalitnější pochopení ekonomických jevů než u některých akademiků).   

Matematika je specifickým druhem jazyka, který se vyvinul jako vhodnější varianta k popisování určitých jevů a k jejich duševnímu zpracování (přemýšlení o nich). Pracuje s abstraktním konceptem čísla, který je prostý veškerých kvalitativních vazeb na objekty, které reprezentuje. Dva hrnce jsou dva hrnce, ať již jsou vnímány jakožto bílé, velké, malé atd. Jsou to dva hrnce dokud spadají do kategorie (množiny) hrnců. (Na základě konceptu čísla matematika poté buduje struktury, u nichž kvalitativní stránku může studovat). Matematika tak přináší do symbolického světa lidské mysli novou dimenzi a sílu. Je zřejmě ještě více „specificky lidská“ než verbální jazyk. Tolik, že s ní mají problémy i samotní lidé :-).

Matematika se ukázala jakožto nepostradatelná pro popis základních vlastností světa kolem nás, které jsou předmětem fyziky. Tyto dvě disciplíny jsou velmi úzce provázané a v běhu lidských dějin se vždy pozitivně ovlivňovaly, zejména směrem od fyziky k matematice. Snaha fyziků o jasné kvantitavní vyjádření svých myšlenek nejednou vedla k rozvoji nových abstraktních struktur v nekonečném matematickém vesmíru či alespoň k blížšímu poznání těch již známých.

Teorie chaosu je relativně mladým odvětvím matematiky, které má velmi blízko k fraktálové teorii a je podmnožinou teorie dynamických systémů. Studuje dynamické systémy (cokoliv, co se vyvíjí v čase), jejichž průběh podstatně závisí počátečních podímkách (parametrech) systému. Jedná se o systémy, které jsou deterministické, tj. lze je popsat bez jakéhokoliv odkazu na náhodné jevy. Přesto vykazují chování, které se zdá být chaotické (nepředvídatelné).

Aby každý pochopil, co to ten „deterministický chaos“ je, uvedeme si ten nejjednodušší (ale velmi kvalitní) příklad tzv. logistického zobrazení.

Mějme dynamický systém popsaný rekurzivní rovnicí x(t+1) = r*x(t)*(1 - x(t)). Hodnoty x(0) jsou v intervalu [0;1], r je kladný parametr. Hodnota v kroku t+1 tak závisí (velice jednoduše) na hodnotě v kroku t a na parametru r. Je jasné, že pokud v kroku t+1 vypočteme stejnou hodnotu jako v kroku t, taková se již bude opakovat stále. To samé platí pro jakkoliv dlouhý úsek hodnot, po němž opět vypočteme jeho první člen. Nic jiného než tento úsek hodnot již nevypočteme. To je determinismus.

Pokud zvolíme x(0) = 0,5 a r = 2, potom x(1) = 2*0,5*(1 - 0,5) = 0,5. Při těchto počátečních podmínkách tak dostaneme konstatní posloupnost, jejíž každý člen je roven 0,5. Pokud zvolíme x(0) = 0,5 a r = 3, máme x(1) = 3*0,5*(1 – 0,5) = 0,75, x(2) = 3*0,75*(1-0,75) = 0,5625 atd. Hodnotám (průběhu) jedné konkrétní posloupnosti (procesu) se říká dráha.

Studium dynamických systémů spočívá zejména v určení, co se stane po „dostatečně dlouhém“ časovém úseku, tj. „dlouhodobě“ (tento pojem může být velmi relativní). K tomu slouží koncept atraktoru, což je množina hodnot, k níž chování (dráha) dynamického systému dlouhodobě směřuje. Tou může být libovolná neprázdná množina a v případě chaotických systémů se jim říká chaotický nebo též podivný atraktor. Často se jedná o fraktály nemající celočíselnou dimenzi. Běžné atraktory se nazývají periodické a perioda označuje počet různých hodnot v daném atraktoru.

Takže nás zajímá, co se děje s posloupností x(t) pro různé hodnoty x(0) a r a pro vysoké hodnoty t. Rádi bychom znali chování systému pro jakoukoliv kombinaci počátečních parametrů. Existuje pro různé dráhy nějaká pravidelnost? S takhle jednoduchou deterministickou rovnicí určitě ano, pravidelnost očekáváme spíše než chaos. K celkovému přehledu nám poslouží níže zobrazený bifurkační diagram logistického zobrazení. Bifurkace je změna periody atraktoru. Nastává například v bodě r = 3, kdy se perioda atraktoru změní z jedné na dva.

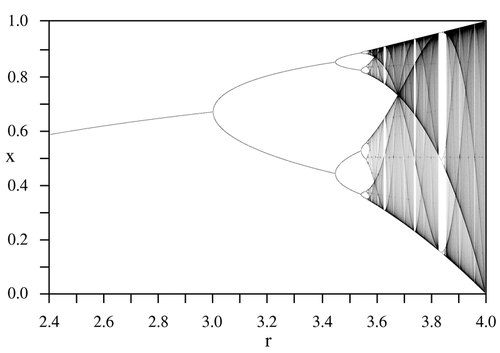
Na svislé ose máme vyneseny hodnoty x a na vodorovné různé hodnoty r. Méně zajímavé hodnoty r nejsou vidět. Jak obrázek „přečíst“? Prvně si zvolte r (např. 2,8) a veďte touto hodnotou svislou kolmici. Tam, kde se tato kolmice protne s grafem, narazíte na „dlouhodobé“ chování posloupnosti, tj. hodnoty, ke kterým (téměř) každá dráha směřuje - atraktor.

Pro r = 2,8 tak bez ohledu na počáteční x(0) posloupnost konverguje k hodnotě přibližně 0,643… Obecně pro r mezi 1 a 3 každá posloupnost bez ohledu na počáteční x(0) konverguje k hodnotě 1 – 1/r. Výjimku tvoří jen dvě nezajímavé hodnoty x(0) = 0 a x(0) = 1, které pochopitelně generují nulové posloupnosti.

Pro r = 3,2 kolmice protne graf ve dvou bodech (přibližně 0,5 a 0,8), dlouhodobě tak posloupnost osciluje mezi těmito hodnotami. Atraktor periody 2 pro r mezi 3 a 3,45 tak tvoří dvě hodnoty téměř bez ohledu na x(0). Každá posloupnoust po určitém počtu kroků začne oscilovat mezi dvěma hodnotami závislými pouze na r. Výjimku zde krom výše zmíněných nudných hodnot 0 a 1 tvoří ještě jeden počáteční bod. Je to bod ležící na křivce předchozího atraktoru, jeho hodnota pro konkrétní r je tedy 1 – 1/r.   

Zatím nic zvláštního, co? Kde je ten „chaos“? Když vezmeme r = 3,5, vidíme, že posloupnost osciluje mezi 4 hodnotami a zdá se, že to tak nudně bude pokračovat dále (8, 16, 32 atd.). Bylo by to čím dál „složitější“, ale ne chaotické. Čím dál tím víc počátečních bodů sice „zlobí“ a jde si svou vlastní cestou mimo atraktor, ale co? Je jich stále jen zanedbatelné množství rovné periodě atraktoru před poslední bifurkací.

Délka intervalu r, kde posloupnost osciluje mezi určitým konstantním počtem hodnot (2, 4, 8, 16 atd.) se sice pořád snižuje, ale celkem předvídatelně. Poměr délek dvou po sobě jdoucích takových intervalů (tj. délka intervalů mezi bifurkacemi) konverguje k Feigenbaumově konstantě (4,6692…). Vypadá to jako hezký dynamický systém, který nebudí ani to zdání chaosu. Ono zmenšování intervalů mezi bifurkacemi jednou ale musí nějak „skončit“, ne?

To se stane pro r přibližně 3,569…, kdy se periodický atraktor vytratí. Dosud ať jsme za x(0) dosadili cokoliv, posloupnost dlouhodobě konvergovala k určitému jasnému počtu hodnot a tyto hodnoty (a jejich počet) závisely pouze na r. Pro r 3,569… toto obecně neplatí a dráha každé konkrétní posloupnosti nyní silně závisí na x(0). Malé změny v x(0) vyvolají nepředvídatelnou změnu v dráze systému. Navíc ta dráha vypadá opravdu zmateně. To je chaos.

Naše krásná posloupnost atraktorů periody 1, 2, 4, 8, 16 atd. tak skončí v hodnotě r = 3,569…, kdy se poprvé projeví chaotický charakter systému. Nyní každá konkrétní posloupnost vypadá „neuspořádaně“ a nepředvídatelně, bez jakéhokoliv náznaku běžné konvergence či oscilace - které tam opravdu nejsou. Každá vypočtená hodnota je jedinečná a už nikdy se v dráze systému nebude opakovat.

Téměř všechny dráhy konvergují k podivnému atraktoru. Tím je v našem případě množina svými (anti-intuitivními) vlastnostmi a strukturou shodná s Cantorovou množinou. Je vskutku podivná, jedná se o fraktál a její Hausdorffova dimenze je rovna přibližně 0,538 (bod je dimenze 0, přímka 1, plocha 2 atd.). Drah nekonvergujících k podivnému atraktoru sice je nyní nekonečně mnoho, ale spočetně nekonečně. To je pro matematiky stále „téměr nic“ :-).

Pro hodnoty r mezi 3,569… a 4 existuje mnoho různých atraktorů, jak periodických, tak chaotických. Podivných atraktorů je tam nespočetně nekonečně mnoho. Existují tam (nechaotické) atraktory s periodou libovolného lichého čísla. Je tam tedy i atraktor periody 3, který sám absolvuje stejnou „zdvojovací“ cestu k chaosu ve formě atraktorů periody 3, 6, 12, 24 atd. Samotný atraktor periody 3 je spolehlivou známkou toho, že dynamický systém bude za určitých podmínek vykazovat chaotické chování.

Je nutné znovu zdůraznit rozdíl mezi náhodností a chaotičností. Logistické zobrazení je perfektně deterministický systém, který však pro určité hodnoty parametru r vykazuje chaotické, nepředvídatelné chování. Atraktor je velmi zvláštní množina, zpravidla fraktál neceločíselné dimenze. Nejedná se však o náhodnou veličinu, k jejímuž popisu by byla vhodná teorie pravděpodobnosti.

Existují samozřejmě i dynamické (chaotické) systémy s prvkem náhody - stochastické dynamické systémy - a též stochastické fraktály. Některé jejich parametry jsou považovány za náhodné veličiny. Stochastické (ale i deterministické) fraktály jsou velmi silným nástrojem pro popis některých „vyšších“ přírodních (např. biologických) jevů. Tyto jevy zpravidla vykazují lokální náhodnost a globální determinismus.

Lidské plíce jsou formovány tak, že se trachea (průdušnice) nejprve rozdělila na dvě větve, ty se opět každá rozdělily na dvě další atd. Jejich délka se zmenšuje podle jistého (rekurzivního) mocninného vztahu, tj. délka následující větve je závislá na délce té předchozí. V každé generaci větví však najdeme určitý rozsah délek a určit, jakou délku bude mít konkrétní větev, lze pouze pravděpodobnostně (tj. s prvkem náhody). Podobným způsobem se formují i stromy a další biologické struktury.

Po malé exkurzi do celkem zajímavého světa moderní matematiky se vrátíme zpět do ještě zajímavějšího světa lidí z masa a kostí, kteří vytvářejí ekonomické fenomény a veličiny. Ekonomické veličiny nejsou výsledkem ani náhodných jevů, ani jevů popsatelných rekurzivními či diferenciálními rovnicemi. Jsou výsledkem rozhodování jednajících, které se odvíjí od jejich subjektivních preferencí a motivací.

Ekonomické fenomény a kategorie jsou specificky lidské, nelze je definovat pojmy z přírodních věd. Spotřebitelé, podnikatelé, vlastníci, zaměstnanci atd. jsou ekonomické role, nikoliv konkrétní osoby. Každá osoba vystupuje v různých rolích. Stejně tak zda-li je určitý statek kapitálový (určený k produkci jiného statku) či spotřební, lze odhalit pouze porozuměním jeho ekonomické roli. Nelze to odhalit jeho fyzikálními, chemickými či technickými charakteristikami. Automobil individuálního podnikatele je spotřebním statkem, když s ním jede na dovolenou, a kapitálovým, když s ním jede na obchodní schůzku nebo pro potřeby do kanceláře.

Produkce a kapitálové statky v rozvintém ekonomickém systému mají velmi komplexní strukturu. Kapitálové statky jsou v čase různě vzdálené od finálních produktů a vzájemně na sobě závisí. Představovat si kapitál jako homogenní hromadu bez jakékoliv vnitřní struktury a časového rozměru, reprezentovanou jediným písmenem „K“ (s nímž se nám dobře počítá), je z analytického hlediska ekvivalentní konceptu, že lidský mozek je jediná buňka.

Veškerá tvrzení obecné ekonomická teorie vždy byla a budou kvalitativního charakteru, protože mezi ekonomickými veličinami neexistují žádné konstantní kvantitativní vztahy, ani jiné podobné stochastického charakteru. Součástí obecné ekonomické teorie nejsou různé oceňovací modely, kvantitativní metody optimalizace produkce atd. To jsou manažerské techniky, které mohou fungovat velmi dobře, protože jsou relativně pokročilejší než techniky používané všeobecně. Nejsou ale ekonomickými zákonitostmi.

Směnné poměry (ceny) jsou jedinými čísly, které jsou důsledkem ekonomického jednání. Jsou jedinými ryze ekonomickými veličinami. Všechna čísla v ekonomii jsou odvozena od cen – nebo jsou neekonomického původu (měrné jednotky). Ceny nejsou generovány mystickými náhodnými procesy. Jsou důsledkem rozhodnutí vstoupit do směny nebo se jí zdržet. Toto rozhodnutí vždy záleží na relativním postavení uvažovaných statků na preferenční škále jedince. Neexistuje způsob, jak toto postavení spolehlivě zjistit, dokud jedinec skutečně nejedná určitým způsobem.

Matematizace ekonomie, která intenzivně započala po 1. čtvrtině 20. století, paradoxně zjednodušila analytickou stránku ekonomie a zároveň s tím se stala zdrojem těch největších ekonomických omylů. Pocit, že celý ekonomický systém (tj. interakci miliard jedinců s různými preferencemi a možnostmi) lze „narvat“ do několika veličin, dvourozměrného grafu, a následně pomocí matematických transformací těchto veličin odhalit novou ekonomickou pravdu, je zřejmě stejně opojný jako pitomý.

Používání matematiky k budování obecné ekonomické teorie zahltilo ekonomii modely s antirealistickými předpoklady, jejichž závěry se - stejně jako jejich předpoklady a zejména metoda – při bližším zkoumání a hlubším přemýšlení ukážou jako scestné. Realitu neviděly ani z vlaku. Většinou končí tam, kam jejich autor chtěl dojít. Neměla by se snad věda snažit popisovat realitu a budovat koncepty, které tomu odpovídají?

Statistice se v ekonomii vyhnout nelze, její místo však leží v ekonomické historii. Po objevení kauzálních kvalitativních vztahů mezi ekonomickými veličinami porozuměním lidskému jednání (např. „zvýšení poptávky ceteris paribus vede ke zvýšení ceny“), lze zkoumat jeden konkrétní historický případ a relativní sílu působících kauzálních faktorů s pomocí statistických metod. „Ceteris paribus“ však v realitě neexistuje a komplexnost celé situace tak téměř vždy ponechá místo pro různé interpretace výsledků.

Budování matematických modelů je k pochopení ekonomických fenoménů zbytečné. Na druhou stranu mne těší alespoň zlepšování v podobě občasné snahy o používání méně nevhodných matematických nástrojů (diskretizace apod.).

Celkem přirozeně se tak nabízí otázka, zda teorie chaosu nebude tou „správnou“ matematikou pro budování ekonomické teorie. Ne, nebude. Ani žádná jiná. Dost možná nějaký zasloužilý akademik obdrží „Nobelovu“ cenu (Cenu Švédské centrální banky) za „revoluční přínos pro ekonomickou analýzu v podobě aplikace nejmodernějších matematických metod k modelování ekonomických jevů“. Bude to hezké matematické cvičení s nulovým přínosem pro obecnou ekonomickou teorii. Možná to však bude kvalitní manažerská technika, jejíž obezřetná aplikace může v konkrétní situaci vést k lepšímu rozhodování a konkurenční výhodě.

Osobně jsem odmalička vždy inklinoval k přírodním vědám a dlouho odmítal samotnou možnost něčeho, co by se dalo nazývat „společenské vědy“. Škádlil jsem své spolužáky ze společenských oborů, aby šli dělat pořádnu vědu (tj. matematiku, fyziku, biologii atd.) a nemrhali svou inteletkovou kapacitu na něco, co jsem vnímal jen jako amorfní chumel arbitrárních tvrzení odvozených od toho, jak se zrovna kdo vyspal.

Často se lze setkat s tvrzením, že ekonomie „leží na rozhraní přírodních a společenských věd“. Zřejmě proto, že ekonomická interakce generuje jeden typ kvantitativní veličiny (cenu), s níž lze provádět tolik kousků! Ekonomie je však ryze lidská a společenská. Přesvědčení, že „používání matematiky“ a „vědeckost“ jsou synonyma, je dětinské. „Vědeckost“ je zaprvé metodologická korektnost a za druhé reálnost.

Comtovská vize „sjednocené, nejvyšší vědy o společnosti“ stále kdekoho okouzluje. Nejzajímavější je tichý a nikým nezpochybňovaný předpoklad, že toto sjednocení by mělo probíhat propůjčením metod a analogií z věd přírodních těm společenským. Vždyť na tu nejnižší neživou hmotu to všechno tak hezky funguje. Teď už docela i na tu živou… hmotu. Ano, lidé sice mají svou vlastní vůli a rozhodování, i když… třeba je to jen iluze, nějaký filozof to říkal. Považovat je za atomy a aplikovat na ně stejné vědecké nástroje zase není takové zjednodušení, ne?